Kì thi tuyển sinh vào lớp 1 chuyên 2009-2010(Cao lãnh)

Đề thi môn Toán cơ sở:

Câu 1: (2 điểm)
a) Rút gọn biểu thức sau :
b) Xác định m và t để hai đường thẳng sau đây trùng nhau:
y = (2 - m)x + (2t +3 - m)

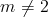
Câu 2: ( 2 điểm)
Cho hình thang ABCD (AB song song với CD) , biết cm ,
BC=6 cm ,góc CAD = 60 độ.Tính CD = ? và tính khoảng cách từ điểm C đường chéo BD.
Câu 3 ;( 2 điểm)
a) Giải hệ phương trình :
b) Tính độ dài 2 cạnh góc vuông của một tam giác vuông , biết rằng nếu tăng các cạnh góc vuông lên 3 cm thì diện tích tam giác đó sẽ
tăng thêm 42 cm vuông và nếu giảm một cạnh góc vuông đi 2 cm và cạnh góc vuông kia giảm đi 4 cm thì diện tích tam giác đó sẽ giảm đi 31 cm vuông.
Câu 4 : ( 2 điểm )
Cho phương trình bậc 2 :
a) Tìm điều kiện m để phương trình (1) có nghiệm.
b) Tìm m sao cho phương trình (1) có 2 nghiệm và thỏa mãn :

Câu 5 : (2 điểm)
Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn (O).Gọi BD, CE là 2 đường cao của tam giác ABC.
a) Chứng minh rằng 4 điểm B , E, D , C cùng nằm trên một đường tròn , xác định tâm I của đường tròn này .
b) Chứng minh rằng : AD.AC=AE.AB
C) Gọi (d) là tiếp tuyến tại A của đường tròn (O). Chứng minh rằng : DE song song với (d)
d) Gọi K là trung điểm của DE.Chứng minh : IK vuông với đường thẳng (d)

Đề toán chuyên

Câu 1:
a) Rút gọn biểu thức :
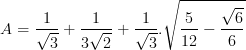
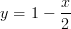
b) Trong mặt phẳng tọa độ Oxy , cho đường thẳng (AB) :.Viết phường trình đường thẳng đi qua C (- 3;0) và vuông góc với đường thẳng (AB) nói trên.
Câu 2 : (2 điểm)
Cho đường thẳng (d) tiếp xúc với đường tròn (O;R) tại A.Trên (d) lấy đoạn thẳng AB= R, tia Bo cắt đường tròn tại C và D ( C nằm giữa B và D).
a) Tính AC và AD theo R.
b) Tính diện tích hình viên phân được giới bởi cung nhỏ AC và dây AC theo R.
Câu 3: ( 2 điểm )
a) Giải hệ phương trình khi m = 1
b) Giải và biện luận hệ phương trình theo tham số m.
Câu 4 : (2 điểm)
Cho phương trình bậc 2 :
Cho hệ phương trình :
a)Chứng minh rằng : phương trình luôn có nghiệm trái dấu với mọi .
b) Với giá trị nào của m phương trình có một nghiệm .Hãy tìm nghiệm còn lại .
Câu 5 : ( 2 điểm )
a) Giải phương trình : (x - 1)(x + 5)(x + 1)(x + 3)=9
b) Cho tam giác ABC cân tại A. Vẽ các đường cao AH, Bk.Chứng minh rằng :