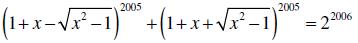Đề tuyển sinh vào lớp 10 Thanh Hoá (2008 - 2009)

Câu 1. (2 điểm)
Cho hai số
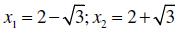
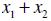
1.Tính và
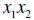
2.Lập phương trình bậc hai ẩn x nhận là hai nghiệm.
Câu 2. (2,5 điểm)
1. Giải hệ phương trình:
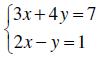
2.Rút gọn biểu thức:
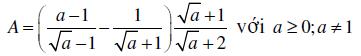
Câu 3. (1 điểm).
Trong mặt phẳng toạ độ Oxy cho đường thẳng (d):y = y = và đường thẳng (d'):y=2x+2. Tìm m để đường thẳng (d) song song với đường thẳng (d').
Câu 4.(3.5 diem).
Trong mặt phẳng cho đường tròn tâm (O), AB là dây cung cô định không đii qua tâm
của đường tròn (O). Gọi I là trung điểm của dây cung AB, M là một điểm nằm trên cung
lớn AB ( M không trùng với A, B). Vẽ đường tròn (O’) đi qua M và tiếp xúc với đường thẳng AB tại A. Tia MI cắt đường tròn (O’) tại điểm thứ hai là N và cắt đường tròn (O) tại điểm thứ hai C.
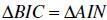
1. Chứng minh rằng:, từ đó chứng minh tứ giác ANBC là hình bình hành.
2. Chứng minh rằng BI là tiếp tuyến của đường tròn ngoại tiếp tam giác BMN.
3. Xác định vị trí của điểm M trên cung AB để diện tích tứ giác ANBC lớn nhất.
Câu 5. (1 điểm)
Tìm nghiệm dương của phương trình: