Bài 1. Tam giác nhọn ABC có trực tâm H. Đường tròn đi qua H với tâm tại điểm giữa của BC
giao với đường BC tại

và
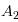
. Tương tự, đường tròn đi qua H với tâm tại điểm giữa của CA
giao với đường CA tại
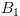
và
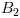
, đường tròn qua H với tâm tại điểm giữa của AB giao với
đường AB tại C1 và C2. Chứng minh rằng
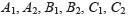
cùng nằm trên một đường tròn.
Bài 2. (a) Chứng minh rằng:

với mọi số thực x, y, z, mỗi số đều khác 1, và thỏa mãn xyz = 1.
(b) Chứng minh rằng đẳng thức xảy ra đối với một số vô hạn bộ ba các số hữu tỷ x, y, z, mỗi
số đều khác 1, và thỏa mãn xyz = 1.
Bài 3. Chứng minh rằng tồn tại vô hạn số nguyên dương n sao cho

có ước nguyên tố lớn hơn
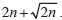 Bài 4.
Bài 4. Tìm tất cả các hàm f : (0,∞) → (0, ∞) (tức là, f là hàm từ tập hợp các số thực dương vào tập hợp các số thực dương) sao cho:
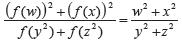
với mọi số thực dương w, x, y, z mà wx = yz.
Bài 5. Giả sử n và k là các số nguyên dương với k ≥ n và k − n là số chẵn. Cho 2n bóng đèn
được đánh số từ 1 đến 2n; mỗi bóng có thể sáng hoặc tắt. Tại thời điểm ban đầu, mọi bóng
đều tắt. Xét các dãy gồm các bước: tại mỗi bước, công tắc của một trong các bóng đèn được
bật (từ sáng chuyển thành tắt hoặc từ tắt chuyển thành sáng).
Giả sử N là số các dãy mà mỗi dãy gồm k bước và kết thúc ở trạng thái: các bóng đèn từ 1 đến
n sáng, các bóng từ n+1 đến 2n tắt.
Giả sử M là số các dãy mà mỗi dãy gồm k bước và cũng kết thúc ở trạng thái: các bóng đèn từ
1 đến n sáng, các bóng từ n+1 đến 2n tắt, nhưng trong quá trình đó không một công tắc nào
của các bóng từ n+1 đến 2n được bật.
Tính tỉ số N/M.
Bài 6 Giả sử ABCD là một tứ giác lồi với |BA| ≠ |BC|. Ký hiệu các đường tròn nội tiếp của
các tam giác ABC và ADC tương ứng qua ω
1 và ω
2. Giả sử tồn tại đường tròn ω tiếp xúc với
nửa đường thẳng BA kéo dài tại một điểm đi sau A và tiếp xúc với nửa đường thẳng BC kéo
dài tại một điểm đi sau C, đồng thời đường tròn đó cũng tiếp xúc với các đường thẳng AD và
CD. Chứng minh rằng các tiếp tuyến chung ngoài của ω1 và ω2 giao nhau tại một điểm nằm
trên đường tròn ω.


