ĐỀ THI OLYMPIC TOÁN QUỐC TẾ 2007

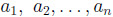
1.Cho .Với mỗi i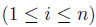đặt:

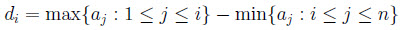
và đặt
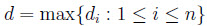
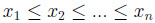
a)Chứng minh rằng ,với mọi số thực tuỳ ý,ta có:

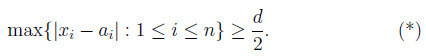
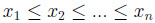
b)Hãy chỉ ra rằng chỉ tồn tại các số thực sao cho bất đẳng thức (*) trở thành đẳng thức.

2.T ìm 5 đi ểm A,B,C,D v à E sao cho ABCD là hình bình hành vàBCED là tứ giác nội tiếp .Cho l là một đường thẳng đi qua A.Giả sử rằng l cắt miền trong của đoạn thẳng DC tại F và cắt đường thẳng BC tại G.Cũng giả sử rằng EF=EG=EC.Chứng minh rằng l là đường phân giác của góc DAB.

3.Trong một kì thi học sinh giỏi môn toán có một thí sinh là bạn bè của nhau.Quan hệ bạn bè luôn là quan hệ hai chiều.gọi một nhóm các thí sinh là nhóm bạn bè nếu như hai người bất kì trong nhóm này là bạn bè của nhau.(Một nhóm tuỳ ý hơn hai thí sinh cũng vẫn được coi là một nhóm bạn bè ).Số lượng các thí sinh của nhóm bạn bè được gọi là cỡ của nó.
Cho biết rằng ,trong kì thi,cỡ của một nhóm bạn bè có nhiều người nhất là một số chẵn.Chứng minh rằng có thể xếp tất cả các thí sinh vào hai phòng sao cho cờ của nhóm bạn bè có nhiều nhất trong phòng này cũng bằng cỡ của nhóm bạn bè có nhiều người nhất trong phòng kia.

4.Trong tam giác ABC , đường phân giác của góc BCA cắt lại đường tròn ngoại tiếp tam giác tại R,cắt đường trung trực của AC tại Q.Trung điểm của BC là K và trung điểm của AC và L.Chứng minh rằng tam giác RPK và tam giác RQL có diện tích bằng nhau.
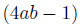
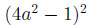
5.Cho trước a và b là hai số nguyên dương .Chứng minh rằng nếu là các ước số của thì a=b.
6.Cho n là một số nguyên dương.Xét:

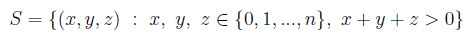
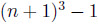
Như là một tập hợp gồm điểm trong không gian 3 chiều.Hãy xác định số nhỏ nhất có thể các mặt phẳng mà hợp của chúng chứa tất cả các điểm của S nhưng không chứa điểm (0,0,0).