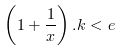Bất đẳng thức Bernoulli

bất đẳng thức Bernoulli là một bất đẳng thức cho phép tính gần đúng các lũy thừa của 1 x.
Bất đẳng thức này được phát biểu như sau:

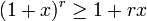
với mọi số nguyên r ≥ 0 và với mọi số thực x > −1. Nếu số mũ r là chẵn, thì bất đẳng thức này đúng với mọi số thực x. Bất đẳng thức này trở thành bất đẳng thức nghiêm ngặt như sau:


với mọi số nguyên r ≥ 2 và với mọi số thực x ≥ −1 với x ≠ 0.

Bất đẳng thức Bernoulli thường được dùng trong việc chứng minh các bất đẳng thức khác. Bản thân nó có thể được chứng minh bằng phương pháp quy nạp toán học:
Chứng minh:
Khi r=0, bất đẳng thức trở thành tức là mà rõ ràng đúng.
Bây giờ giả sử bất đẳng thức đúng với r=k:

Cần chứng minh:

Thật vậy, (vì theo giả thiết ) (vì )

=> Bất đẳng thức đúng với r=k 1.

Theo nguyên lý quy nạp, chúng ta suy ra bất đẳng thức đúng với mọi

Số mũ r có thể tổng quát hoá thành số thực bất kỳ như sau: nếu x > −1, thì


với r ≤ 0 or r ≥ 1, và


với 0 ≤ r ≤ 1.

Có thể chứng minh bất đẳng thức tổng quát hoá nói trên bằng cách so sánh các đạo hàm.

Một lần nữa, bất đẳng thức này trở thành bất đẳng thức nghiêm ngặt nếu x ≥ -1 và 1 ≤ r thuộc tập số tự nhiên.

Các bất đẳng thức liên quan

Bất đẳng thức dưới đây ước lượng lũy thừa bậc r của 1 x theo chiều khác. Với số thực x bất kỳ, r > 0, chúng ta có


với e = 2.718.... Bất đẳng thức này có thể chứng minh bằng cách dùng bất đẳng thức