Chuyên đề 1: Số chính phương

I Khái niệm:
- Số chính phương là số bằng bình phương của một số tự nhiên.
- Mười số chính phương đầu tiên là: 0,1,4,9,16,25,36,49,64,81,...
II Tính chất:
- Số chính phương không tận cùng bởi các chử số: 2,3,7,8
- Khi phân tích một số chính phương ra thừa số nguyên tố ta được các thừa số là lũy thừa của số nguyên tố với số mũ chẳn.
Chẳng hạn:
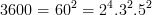
Từ đó:
- Số chính phương chia cho 3 chỉ có thể dư 0 hoặc 1.
- Nếu hai số nguyên liên tiếp có tích là một số chính phương thì một trong hai số nguyên đó là số 0.
III Nhận biết:
a) Để chứng minh N là một số chính phương của một số tự nhiên (hoặc số nguyên).
- Vận dụng tính chất: nếu hai số tự nhiên a và b nguyên tố cùng nhau có tích là một số chính phương thì mỗi số a, b cũng là một số chính phương.
b) Để chứng minh N không phải là số chính phương ta có thể:
- Chứng minh N có chữ số tận cùng là 2,3,7,8.
- Chứng minh N chứa số nguyên tố với mũ lẽ.
- Xét số dư khi N cho 3 hoặc cho 4 hoặc cho 5 cho 8.
- Chứng minh N nằm giửa hai số chính phương liên tiếp.
* N chia cho 3 dư 2; N chia cho 4; 5 có số dư là 2; 3.
suy ra N không phải là số chính phương